Variation of properties in the dense phase region; Part 2 – Natural Gas

In the last tip of the month (TOTM) we described the dense phase of a pure compound and how it impacted processes. We illustrated how thermophysical properties change in the dense phase as well as in the neighboring phases. The application of dense phase in the oil and gas industry was discussed briefly. In this TOTM, we will discuss the dense phase behavior of multi-component systems, like natural gases.

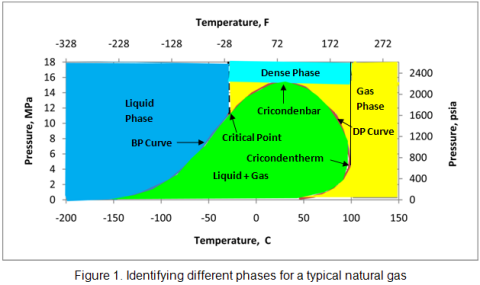
When a natural gas, is compressed above the cricondenbar in the region between critical temperature andcricondentherm, it becomes a dense, highly compressible fluid that demonstrates properties of both liquid and gas. Figure 1 presents different regions of the phase envelope for a typical natural gas mixture with the composition shown in Table 1.

Table 1. Composition of the natural gas used in this study

For simplicity and convenience, we define the dense phase to be within critical temperature and cricondentherm if the pressure is above the cricondenbar. In practice, there is no clear line (i.e. critical temperature) dividing dense phase from liquid phase or other single line (i.e. cricondentherm) dividing the dense phase from the gas phase. Both the left bound (critical temperature) and the right bound (cricondentherm) should be replaced by a transition region. There is a gradual transition from the gas phase to the dense phase and another gradual transition from the dense phase to the liquid phase. The dense phase is often referred to as a “dense fluid” to distinguish it from normal gas and liquid (see Figure 1). Dense phase is a fourth (Solid, Liquid, Gas, Dense) phase that cannot be described by the senses. The word “fluid” refers to anything that will flow and applies equally well to gas and liquid. The dense phase has a viscosity similar to that of a gas, but a density closer to that of a liquid. Because of its unique properties, dense phase has become attractive for transportation of natural gas.

Pipelines have been built to transport natural gas in the dense phase region due to its higher density. This also provides an added benefit of no liquids formation in the pipeline, reducing pigging and pressure drop which results in lower OPEX. The higher density at higher pressure in the dense phase allows transporting more mass per unit volume, resulting in higher CAPEX. However, the OPEX reduction usually offsets the CAPEX increment.  As shown in the following sections, the value of the dense phase viscosity is very similar to gas phase viscosity. The dense phase density is closer to the liquid phase density.
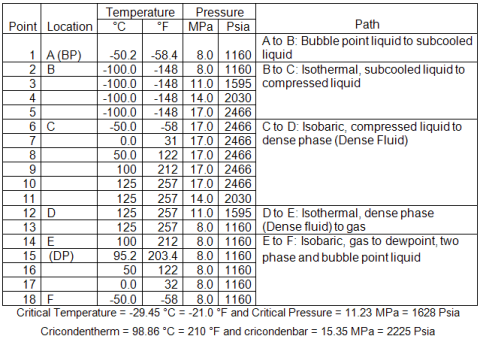
In the next section we will illustrate the variation of thermophysical properties in the dense phase and its neighboring phases. Natural gas properties have been calculated with HYSYS software for a series of temperatures and pressures. Table 2 presents, the pressures and temperatures and their paths used in this study.
The calculated thermophysical properties are plotted as a function of pressure and temperature in Figures 2 to 9. The thermophysical property is shown on the left-hand side y-axis, temperature on the x-axis and pressure on the right-hand side y-axis.

Table 2. Pressure-Temperature combination and the paths chosen for natural gas

Density:
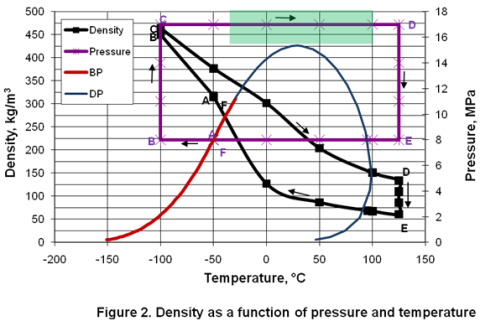
Figure 2 presents the variation of density in different phases as a function of pressure and temperature. In the isobaric subcooling path of AB, liquid density increases sharply. However, in the isothermal compression of BC path, a small increase of density is observed. In the isobaric CD path, compressed liquid density decreases gradually as temperature is increased well into the dense phase region. However, as the temperature increases further in the dense phase, density reduction is accelerated. Reduction of density is further accelerated during isothermal expansion of DE. Isobaric cooling of gas along EF path corresponds with a sharp increase in density. It can be noted the values of dense phase density are close to the liquid phase density in some areas of the dense phase region, and is overall significantly higher than the gas phase densities.

Viscosity:
Figure 3 presents the variation of viscosity in different phases as a function of pressure and temperature. In the isobaric subcooling path of AB, liquid viscosity increases sharply. However, in the isothermal compression of BC path, a very small change of viscosity is observed. In the isobaric CD path, compressed liquid viscosity decreases linearly and sharply as temperature is increased well into the dense phase region. As the temperature increases further in the dense phase, viscosity reduction becomes gradual and approaches the gas phase values. Reduction of viscosity is quite small during isothermal expansion of DE. Isobaric cooling of gas along EF path up to the dew point temperature corresponds with no appreciable change in viscosity but increases noticeably in the two phase region. For the sake of completing the graph, the two phase viscosity was estimated by: where (V/F) and (L/F) are vapor and liquid mole fractions, respectively.

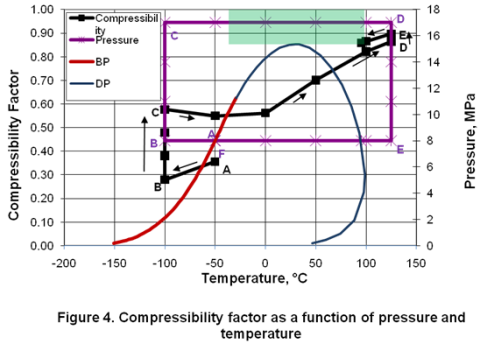
Compressibility Factor:
In general, the compressibility factor, Z, calculated by an equation of state is not accurate for the liquid phase. Therefore, Figure 4 which presents compressibility factor as a function of pressure and temperature should be considered for qualitative study only. In the isobaric subcooling path of AB, Z decreases. However, in the isothermal compression of BC path, Z increases drastically. In the isobaric CD path, Z remains almost constant in the compressed liquid region but increases gradually as temperature is increased well into the dense phase region. As the temperature increases further in the dense phase, the increase in Z is accelerated. The increase in Z is further accelerated during isothermal expansion of DE. Isobaric cooling of gas along EF path corresponds with a gradual decrease in Z. In the two-phase region, Z is not applicable and its value is not plotted.

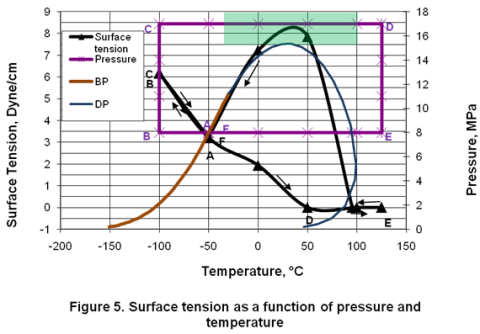
Figure 5 shows that in the liquid phase, surface tension is a strong function of temperature but independent of pressure. In the gas phase, surface tension is not applicable and its value is zero. In the two-phase region, it reached a maximum value.

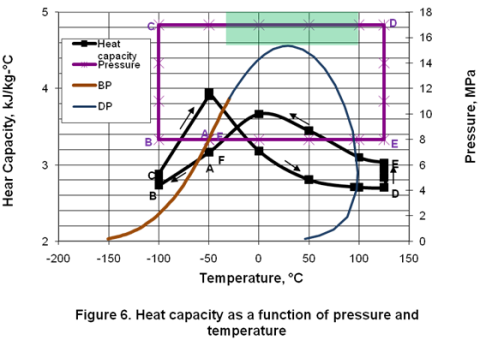
Heat Capacity:
Generally, heat capacity is applicable in a single phase region and should not be used when there is a phase change. Figure 6 presents the variation of heat capacity in different phases as a function of pressure and temperature. In the isobaric subcooling path of AB, liquid heat capacity decreases. In the isothermal compression of BC path, a small increase of heat capacity is observed. In the isobaric CD path, compressed liquid heat capacity increases sharply as temperature is increased but starts to decrease in the dense phase region. As the temperature increases further in the dense phase, heat capacity decreases. This is strange behavior and surprisingly high values are calculated. Similar results were obtained for pure methane in the previous TOTM. Increase of heat capacity is further noticed during isothermal expansion of DE. Isobaric cooling of gas along EF path corresponds with a gradual increase in heat capacity up to a maximum point and then starts to decrease in the two phase region.

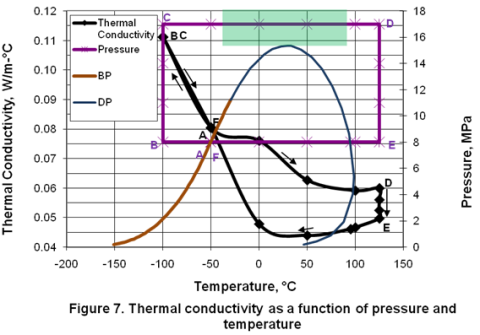
Thermal Conductivity:
Figure 7 presents the variation of thermal conductivity in different phases as a function of pressure and temperature. In the isobaric subcooling path of AB, liquid thermal conductivity increases sharply. In the isothermal compression of BC path, no change is observed. In the isobaric CD path, compressed liquid thermal conductivity decreases sharply as temperature is increased well into the dense phase region. However, as the temperature increases further in the dense phase, thermal conductivity reduction is gradual. Reduction of thermal conductivity is further noticed during isothermal expansion of DE. Isobaric cooling of gas along EF path corresponds with a small decrease in thermal conductivity and goes up in the two-phase region. The two-phase thermal conductivity was calculated in the same manner as described in the viscosity section.

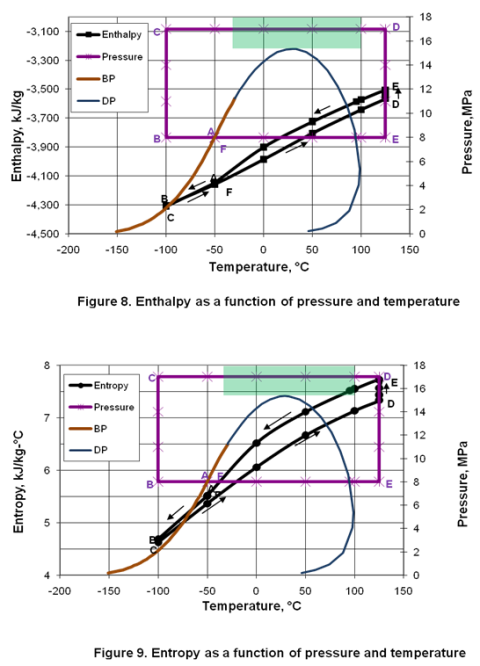
Enthalpy and Entropy:
Figures 8 and 9 present the variation of enthalpy and entropy in different phases as a function of pressure and temperature. As shown in these figures, their qualitative variations are similar. In the isobaric subcooling path of AB, liquid enthalpy and entropy decrease. In the isothermal compression of BC path, no change is observed. During the isobaric CD path, compressed liquid enthalpy and entropy values increase gradually as temperature is increased well into the dense phase region. The increase in enthalpy and entropy is further noticed during isothermal expansion of DE. Isobaric cooling of vapor along EF path corresponds with a decrease in enthalpy and entropy.

Conclusions:
Dense phase behavior is unique and has special features. The thermophysical properties in this phase may vary abnormally. Care should be taken when equations of state are used to predict thermophysical properties in dense phase. Evaluation of equations of state should be performed in advance to assure their accuracy in this region. Many simulators offer the option to use liquid-based algorithms (e.g. COSTALD) for this region. It is also recommended not to use heat capacity in the two-phase (gas-liquid) and in the dense phase. In these regions, enthalpy should be used for heat duty and energy balance calculations.
There is a gradual change of phase transition from gas-to-dense and dense-to-liquid phases or vice versa. Dense phase is a highly compressible fluid that demonstrates properties of both liquid and gas. The dense phase has a viscosity similar to that of a gas, but a density closer to that of a liquid. This is a favorable condition for transporting natural gas in dense phase.
To learn more about similar cases and how to minimize operational problems, we suggest attending our G-40 (Process/Facility Fundamentals), G-4 (Gas Conditioning and Processing), PF-81 (CO₂ Surface Facilities), and PF-4 (Oil Production and Processing Facilities) courses.

John M. Campbell Consulting (JMCC) offers consulting expertise on this subject and many others. For more information about the services JMCC provides, visit our website at www.jmcampbellconsulting.com, or email your consulting needs to consulting@jmcampbell.com.

By: Dr. Mahmood Moshfeghian

Reference:

1. ASPENone, Engineering Suite, HYSYS Version 2006, Aspen Technology, Inc., Cambridge, Massachusetts U.S.A., 2006.