Which Equations of State Should be Used for Compressor Calculations?

In the November tip of the month (TOTM) we presented a single-stage compressor calculation result of a case study. We compared the rigorous method with the values from the short cut methods. The rigorous method was based on the Soave-Redlich-Kwong (SRK) for calculating the required enthalpies and entropies.

In this TOTM, we will present a case study of multistage stage compression with interstage cooling using the rigorous method. The rigorous method will be based on the Soave-Redlich-Kwong (SRK), Peng-Robinson (PR), Lee Kesler (LK) and Benedict-Webb-Rubin-Starling (BWRS) equations of state. The K-values, enthalpies, and entropies are calculated by these EOSs to perform vapor-liquid-equilibrium (VLE) and the energy balance calculations to determine the power requirement, the discharge temperatures and the cooling load requirements. We will compare the compressor power and cooling load requirements based on the rigorous equations of state.

Power Calculations

The theoretical power requirements are independent of compressor type; the actual power requirements vary with the compressor efficiency. In general the power is calculated by:

From a calculation viewpoint alone, the power calculation is particularly sensitive to the specification of flow rate, inlet temperature and pressure, and outlet pressure. Gas composition is important but a small error here is less important providing it does not involve the erroneous exclusion of corrosive components. A compressor is going to operate under different values of the variables affecting its performance. Therefore the most difficult part of a compressor calculation is specification of a reasonable range for each variable and not the calculation itself. Reference [1] emphasizes that using a single value for each variable is not the correct way to evaluate a compression system.

Normally, the thermodynamic calculations are performed for an ideal (reversible) process. The results of a reversible process are then adapted to the real world through the use of efficiency. In the compression process there are three ideal processes that can be visualized: 1) an isothermal process, 2) an isentropic process and 3) a polytropic process. Any one of these processes can be used suitably as a basis for evaluating compression power requirements by either hand or computer calculation. The isothermal process, however, is seldom used as a basis because the normal industrial compression process is not even approximately carried out at constant temperature.

Step-by-Step Computer Solution

For known gas rate, pressure (P₁), temperature (T₁), and composition at the inlet condition and discharge pressure (P_2­) or compression ratio, computation of compressor power requirement is based on an EOS using a computer and involves two steps:

1. Determination of the ideal or isentropic (reversible and adiabatic) enthalpy change of the compression process. The ideal work requirement is obtained by multiplying mass rate by the isentropic enthalpy change.
2. Adjustment of the ideal work requirement for compressor efficiency.
   The step-by-step calculation based on an EOS is outlined below.
   1. Assume steady state, i.e. 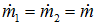  and the feed composition remain unchanged.
   2. Assume isentropic process, i.e. adiabatic and reversible
   3. Calculate specific enthalpy h₁=f(P₁, T₁, and composition) and suction specific entropy s₁=f(P₁, T₁, and composition) at the suction condition by EOS
   4. For the isentropic process 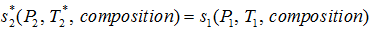. Note the * represents ideal value.
   5. Calculate the ideal specific enthalpy 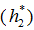 at outlet condition for known composition, P₂ and .
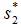   6. The ideal work is 
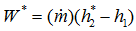
   7. The actual work is the ideal work divided by efficiency or 
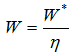
   8. The actual enthalpy at the outlet condition is calculated by 
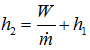
   9. The actual outlet temperature is calculated by EOS for known h₂, P₂, and composition.

The efficiency of the compressor, and hence, the compression process obviously depends on the method used to evaluate the work requirement. The isentropic efficiency is in the range of 0.70 to 0.90.

If the manufacturer provides the compressor head curve and efficiency curve, the head is determined from the actual gas volume rate at the inlet condition. Second, from the head, the actual work, discharge pressure and finally the discharge temperature are calculated.

Case Study

The gas mixture with the composition shown in Table1 at 105 °F (40.6 °C) and 115 Psia (793 kPa) is compressed to 1015 psia (7000 kPaa) using a multistage centrifugal compressor. The total feed gas volumetric flow rate was 101 MMSCFD (2.86×10⁶ Sm³/d). This is the same feed used in the November TOTM.

Table 1. Feed gas analysis

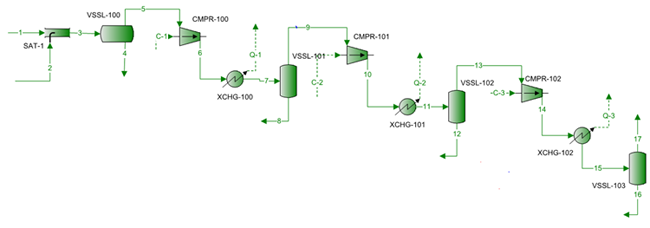
A simplified process flow diagram is shown in Figure 1. The dry feed gas is saturated with water, passed through a scrubber (knockout drum) before entering the first stage of compressor. Each compression stage is followed by cooling and subsequent knockout drum before entering the next stage. An equal compression ratio of 3 was used for each stage. The polytropic efficiency of 86, 80, and 79 % based on the actual inlet volumetric rate (from Figure 13.23 of GPA Data book [2]) was specified for stages 1, 2, and 3 respectively. After each compression stage, the gas was cooled to the feed temperature of 105 °F (40.6 °C).

Figure 1. Three-stage compression with interstage cooling

Results and Discussions

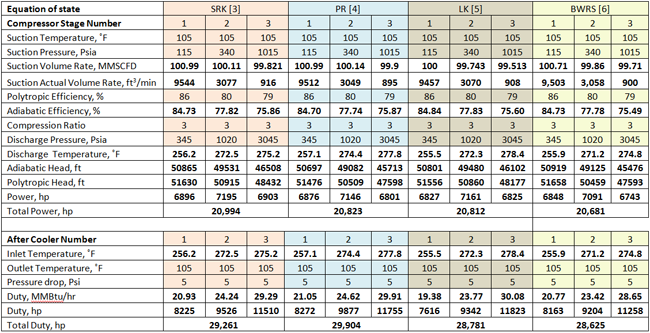
The feed composition, suction temperature and pressure, volumetric flow rate at standard condition along with the compressor polytropic efficiency for each stage, and pressure drop for each cooler were specified. For this study, the above PFD was simulated using the Soave-Redlich-Kwong (SRK) [3], Peng-Robinson (PR) [4], Lee Kesler (LK) [5] and Benedict-Webb-Rubin-Starling (BWRS) [6] equations of states. These data were entered into the ProMax software [7] to perform the rigorous calculations based on the EOS. The program calculated discharge temperature, power for each stage, and cooling loads for each cooler. For the actual gas flow rate at the inlet condition, the polytropic efficiency was specified from the GPA data book. The calculated results for the four EOSs are presented in Table 2 (bold numbers with white background).

Table 2 (FPS units). Summary of the rigorous results for four EOSs using ProMax

The bold numbers with white background are the calculated values

 

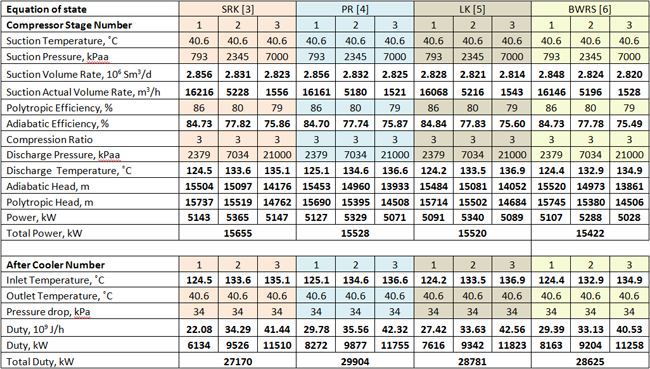
Table 2 (SI Units). Summary of the rigorous results for four EOSs using ProMax

The bold numbers with white background are the calculated values

For the case of LK EOS, the wet feed volume flow rate at standard condition to the first stage of compressor is lower than the other cases because this EOS has not been revised to handle water content.

For the case studied, Table 2 indicates that there is 0.8 to 1.4 percent deviation in total compression power requirements among these 4 EOSs. The deviation in total heat removal using different EOSs is 1.7 to 2.2 percent. For facility type calculations and planning purposes, these differences are negligible. However, for cases with large power requirement, these small differences in terms of total HP or kW could be significant; therefore, care should be taken to choose an appropriate EOS for handling VLE calculations and accurate predictions of enthalpy and entropies for the system under consideration. The deviation range could be different for other cases depending on the flow rates, condition composition and compression ratio.

To learn more about similar cases and how to minimize operational problems, we suggest attending the John M. Campbell courses; G4 (Gas Conditioning and Processing), G5 (Gas Conditioning and Processing-Special) and ME 44 (Fundamentals of Pump and compressors).

John M. Campbell Consulting (JMCC) offers consulting expertise on this subject and many others. For more information about the services JMCC provides, visit our website at www.jmcampbellconsulting.com, or email your consulting needs to consulting@jmcampbell.com.

By Dr. Mahmood Moshfeghian

References:

1. Maddox, R. N. and L. L. Lilly, “Gas conditioning and processing, Volume 3: Advanced Techniques and Applications,” John M. Campbell and Company, 2^nd Ed., Norman, Oklahoma, USA, 1990.
2. Gas Processors Association Data Book, 12^th Edition, GPA, Tulsa, Oklahoma.
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.
5.  Lee B.I., Kesler M.G., “A Generalized Thermodynamic Correlation Based on Three-Parameter Corresponding States”, AIChE J., 21(3), 510-527, 1975
6. Starling, K. E., Fluid Thermodynamic Properties for Light Petroleum Systems,  Gulf Publishing Co., Houston, 1973.
7. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2011.