In this tip of the month (TOTM) we will discuss transportation of carbon dioxide (CO2) in the dense phase. We will illustrate how thermophysical properties change in the dense phase and their impacts on pressure drop calculations. The pressure drop calculations results utilizing the liquid phase and vapor phase equations will be compared. The application of dense phase in the oil and gas industry will be discussed briefly. In a future TOTM, we will discuss the dense phase transportation of natural gas.
When a pure compound, in gaseous or liquid state, is heated and compressed above the critical temperature and pressure, it becomes a dense, highly compressible fluid that demonstrates properties of both liquid and gas. For a pure compound, above critical pressure and critical temperature, the system is oftentimes referred to as a “dense fluid” or “super critical fluid” to distinguish it from normal vapor and liquid (see Figure 1 for carbon dioxide in December 2009 TOTM [1]). Dense phase is a fourth (Solid, Liquid, Gas, Dense) phase that cannot be described by the senses. The word “fluid” refers to anything that will flow and applies equally well to gas and liquid. Pure compounds in the dense phase or supercritical fluid state normally have better dissolving ability than do the same substances in the liquid state. The dense phase has a viscosity similar to that of a gas, but a density closer to that of a liquid. Because of its unique properties, dense phase has become attractive for transportation of CO2 and natural gas, enhanced oil recovery, food processing and pharmaceutical processing products.
The low viscosity of dense phase, super critical carbon dioxide (compared with familiar liquid solvents), makes it attractive for enhanced oil recovery (EOR) since it can penetrate through porous media (reservoir formation). As carbon dioxide dissolves in oil, it reduces viscosity and oil-water interfacial tension, swells the oil and can provide highly efficient displacement if miscibility is achieved. Additionally, substances disperse throughout the dense phase rapidly, due to high diffusion coefficients. Carbon dioxide is of particular interest in dense-fluid technology because it is inexpensive, non-flammable, non-toxic, and odorless. Pipelines have been built to transport CO2 and natural gas in the dense phase region due to its higher density, and this also provides the added benefit of no liquids formation in the pipeline.
In the following section we will illustrate the pressure drop calculations for transporting CO2 in dense phase using liquid phase and vapor phase pressure drop equations.
Case Study:
For the purpose of illustration, we considered a case study for transporting 160 MMSCFD (4.519×106 Sm3/d) CO2 using a 100 miles (160.9 km) long pipeline with an inside diameter of 15.551 in (395 mm). The corresponding mass flow rate is 214.7 lbm/sec (97.39 kg/s). The inlet conditions were 2030 psia (14 MPa) and 104˚F (40˚C). The following assumptions were made:
- Pure CO2, ignored any impurities such as N2.
- Horizontal pipeline, no elevation change.
- Inside surface relative roughness (roughness factor), ε/D, is 0.00004.
- Isothermal transportation of CO2.
Properties: Dense phase behavior is unique and has special features. The thermophysical properties in this phase may vary abnormally. Care should be taken when equations of state are used to predict thermophysical properties in dense phase. Evaluation of equations of state should be performed in advance to assure their accuracy in this region. Many simulators offer the option to use liquid-based algorithms (e.g. COSTALD [2]) for this region. Dense phase is a highly compressible fluid that demonstrates properties of both liquid and gas. The dense phase has a viscosity similar to that of a gas, but a density closer to that of a liquid. This is a favorable condition for transporting CO2 and natural gas in dense phase as well as carbon dioxide injection into crude oil reservoir for enhanced oil recovery.
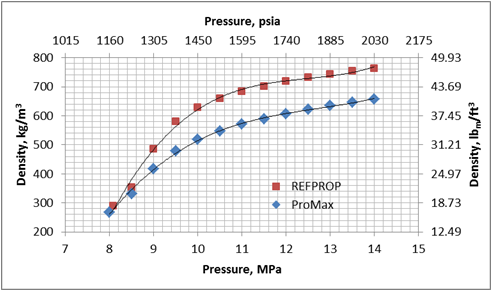
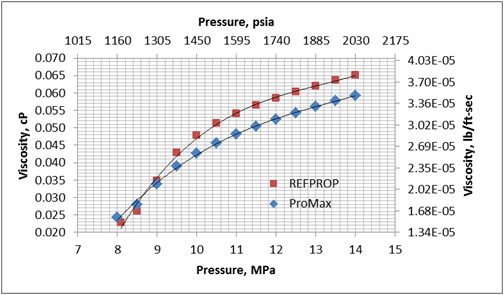
Figures 1 and 2 present variation of density and viscosity of CO2 with pressure at constant temperature of 104 ˚F (40 ˚C) calculated by the SRK EOS and COSTALD liquid density option in ProMax [3] and the Span and Wagner CO2 EOS in REFPROP [4] software. Note, ProMax also has the Span and Wagner CO2 EOS option which produced practically the same results as the REFPPROP.
Figure 1. Density-Pressure diagram for CO2 at 104˚F (40˚C) by the SRK EOS and COSTALD liquid in ProMax and Span and Wagner CO2 EOS in REFPROP
Figure 2. Viscosity-Pressure diagram for CO2 at 104˚F (40˚C) by the SRK EOS and COSTALD liquid in ProMax and Span and Wagner CO2 EOS in REFPROP
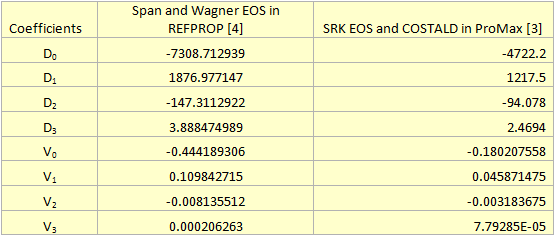
For the sake of easier calculation steps, these diagrams were fitted to the following 3rd degree polynomials for density and viscosity, respectively:
In these equations, ρ is density (kg/m3), µ is viscosity (cP) and Pavg is the average pipeline segment pressure calculated by:
The fitted coefficients for equations 1 and 2 are presented in Table 1.
Table 1. The fitted coefficients for CO2 density and viscosity (Equations 1 & 2) at 104˚F (40˚C)
Figures 1 and 2 clearly indicate that there are large differences between predicted properties using two different sources. In the following section, we will illustrate the impact of these differences on pressure drop calculations.
Liquid Phase Pressure Drop Equations: The pressure drop for a liquid phase is calculated as follows.
Where:
Vapor Phase Pressure Drop Equations: In addition to Equations 5 through 8, which are also valid and used for the gas pipeline, the following equations are also used.
Where:
Results and Discussions:
The pressure drop calculations were performed using the liquid phase and vapor phase equations. First, the pipeline cross sectional area was calculated with Equation 8 and the gas density at the standard condition was calculated with equation 10. In each case the calculation was trial and error and the following step-by-step procedure was followed:
- The line was divided into n segments (e.g. n = 1, 10, 20, or 100).
- For segment 1, an outlet pressure was guessed.
- Segment average pressure was calculated with Equation 3.
- CO2 density and viscosity were calculated using Equations 1 and 2, respectively.
- CO2 velocity was calculated with Equation 7.
- Reynolds number was calculated with Equation 6.
- Friction factor was calculated with Equation 5 (this is also trial and error).
- Liquid phase pressure drop was calculated with equation 4.
- Calculate average gas compressibility factor with equation 11.
- Calculate segment gas outlet pressure by Equation 9 and segment pressure drop with Equation 12.
- If the calculated outlet pressure is not the same as the guessed outlet pressure in step 2, replace the guessed outlet pressure with the calculated outlet pressure and repeat steps 3 through 10 until the calculated outlet pressure becomes equal to the guessed value.
- Use the calculated outlet pressure of segment “1” for the inlet of segment “2” and repeat the above steps for each segment till the end of line is reached.
Table 2 summarizes the pressure drop calculation results for four cases in which the pipeline was divided into 1, 10, 20, and 100 segments. Table 2 indicates that for the cases of 10 segments and higher no change in pressure drop is observed.
Table 2. Summary of pressure drop calculation results for different number of segments and different sources of properties.

For all cases tested, both the liquid phase and the vapor phase pressure drop equations gave exactly the same pressure drop. Note that there is at least 100 psi (690 kPa) difference in pressure drops calculation using REFPROP (Span and Wagner CO2 EOS) or ProMax (SRK EOS and COSTALD liquid density) because the EOS options were different. However, the Span and Wagner CO2 EOS in both software would result in the same pressure drop. A sample calculation in MathCad format is attached: Dense Phase CO2 Pipeline 1 Segment ProMax.
Table 3 presents the impact of relative roughness on pressure drop. Typical / generally accepted numbers for relative roughness are (and these are regarded as conservative) for steel pipes are: new or clean service = 0.00004, mildly corroded = 0.0002, corroded / dirty service = 0.0004.
Table 3. Impact of relative roughness on pressure drop (Number of segments=10).
Conclusions:
As discussed in December 2009, dense phase behavior is unique and has special features. The thermophysical properties in this phase may vary abnormally. Care should be taken when equations of state are used to predict thermophysical properties in dense phase. Evaluation of equations of state should be performed in advance to assure their accuracy in this region. Many simulators offer the option to use liquid-based algorithms (e.g. COSTALD) for this region. It is very important to use the most appropriate option.
Dense phase is a highly compressible fluid that demonstrates properties of both liquid and gas. The dense phase has a viscosity similar to that of a gas, but a density closer to that of a liquid. This is a favorable condition for transporting CO2 and natural gas in dense phase. It was also found that either the liquid phase or vapor phase pressure drop equations can be used to calculate CO2 pressure drop in the dense phase. Both set of equations gave exactly the same pressure drop. Due to high density of CO2 in the dense phase, pressure drop due to elevation change should not be ignored.
To learn more about similar cases and how to minimize operational problems, we suggest attending our G40 (Process/Facility Fundamentals), G4 (Gas Conditioning and Processing), P81 (CO2 Surface Facilities), and PF4 (Oil Production and Processing Facilities) courses.
By: Dr. Mahmood Moshfeghian
Reference:
- Bothamley, M.E. and Moshfeghian, M., “Variation of properties in the dese phase region; Part 1 – Pure compounds,” http://www.jmcampbell.com/tip-of-the-month/2009/12/variation-of-properties-in-the-dense-phase-region-part-1-pure-compounds/, December 2009.
- Hankinson, R. W., Thomson, G. H., AIChE J., Vol. 25, no. 4, pp. 653-663, 1979.
- ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2011.
- NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP): Version 9.0, 2011.


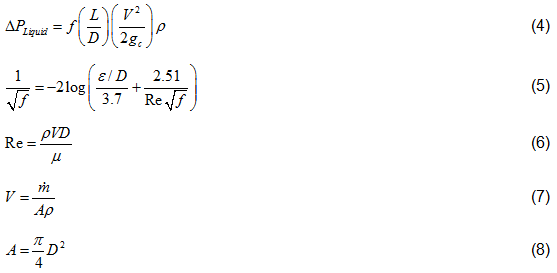





This TOTM shows that large differences are obtained in the dense phase properties when using the two references studied in this paper and comments as follows:
“Care should be taken when equations of state are used to predict thermophysical properties in dense phase. Evaluation of equations of state should be performed in advance to assure their accuracy in this region”.
The easy way for the designer would be to always use the most conservative results when specifying a process operating in dense phase but it may become costly. Any suggestion on how to validate whether the less conservative results can be used safely?
I think the primary recommendation is to validate your properties model. If you don’t do any validation, then how do you know if your design is conservative or not – and by how much?
For the fun of it, I re-ran this design example assuming the densities were actually 10% lower than predicted by the Span & Wagner EOS. Viscosity values were used directly from the Span & Wagner EOS.
The pressure drop I calculate for the 100 mile pipeline increased from 273 psi (1.88 MPa) to approximately 301 psi (2.08 MPa) with a relative roughness of 0.00004. I can then decide if my system can tolerate that much variation. If not, I may want to do some work to ensure my properties predictions are sufficiently accurate.
Your question is a good one, even if you do validate your fluids properties model. This example assumes 100% pure CO2. None of the existing CO2 pipelines that I am aware of contain 100% pure CO2. There are always contaminants. From my experience, the Span & Wagner EOS does an excellent job of predicting properties of pure CO2, but it is not applicable for multi-component systems.
So what happens if the CO2 is not pure? I can validate my fluid model (something other than Span & Wagner), but what if the assumed composition is wrong or if the composition changes over time?
One of the advantages of computer-based design, is that I can, with relative ease, evaluate the sensitivity of my system to different fluid compositions and/or evaluate the impact of inaccurate data. In some cases, better properties prediction may be necessary to avoid over-spending on the pipeline. In other cases, over-building may be necessary to accommodate the unknown or unknowable.
Something to add, SRK provides relatively poor results in the dense phase region for CO2. In any simulator, including ProMax, if you have a stream containing some contaminants such as methane, water, N2, etc. (thereby making Span and Wagner unusable), Peng-Robinson is an inherently more accurate EOS for dense phase CO2. See the image below:
http://i1150.photobucket.com/albums/o611/laddington/Densities.jpg
COSTALD is a liquid density method and, although we may have a fluid that has liquid-like properties, it is not appropriate to apply this method to our dense phase stream. The molar volume values coming out of the equation-of-state are suitable for the vapor and “dense” phases; they do not need correction by COSTALD or RACKETT.
ProMax does not have a phase titled “dense” and must therefore define the stream either as a vapor or a liquid when it is above the critical. COSTALD is only applied to the liquid, so as long as the stream is being called a vapor (and it is defined as a vapor in ProMax over the range presented by Mahmoud) the EOS is actually being used, regardless of the settings applied. The densities displayed in Figure 1, therefore, were not calculated using COSTALD, rather they are being predicted by the SRK EOS.
As Mahmoud said, it is important to understand where the predictions are as compared to data. This is true for any system, but especially true for this one. Ms. Castel is right that we would prefer to be conservative, but there’s a fine line between being conservative and being incorrect. Errors on densities of 15-20% can be detrimental when considering, for example, elevation changes in pipelines. This is especially true for injection wells which may have an elevation change of tens of thousands of feet. So even if a more “conservative” method is accepted, it is still important to know how conservative. We would like to have predictions as close to the correct answer as possible, understand the deficiencies and “unknowns” in the predictions, as Wright described, and then apply our engineering judgment to obtain a feasible, safe design.
Mainly interested in compression, heat transfer, fluids and any mathematical models in relation to them.
i have question please when i use the equation of agas to calculate po the output differ to what you calculate in Dense Phase CO2 Pipeline 1 Segment ProMax. please i want to know the dimension for the length & diameter
Transportation of CO2 in Dense Phase | Campbell Tip of the Month
roger vivier sale http://www.hardingalumni.org/rv.htm/
always i used to read smaller posts that as well clear their motive,
and that is also happening with this paragraph which I am reading now.