Non-Isothermal Transportation of CO2 in the Dense Phase

 In the January 2012 tip of the month (TOTM) we discussed the isothermal transportation of carbon dioxide (CO₂) in the dense phase. We illustrated how thermophysical properties changed in the dense phase and studied their impacts on pressure drop calculations. The pressure drop calculation results utilizing the liquid phase and vapor phase equations were exactly the same. In this TOTM, we will study the same case study under non-isothermal conditions. The Joule-Thompson expansion effect and the heat transfer between pipeline and surroundings have been considered. Specifically, we will report the effects of the overall heat transfer coefficient and the relative roughness on the pressure and temperature profiles. The Span and Wagner CO₂ equation of state (EOS) was utilized in this study.

For a pure compound, above critical pressure and critical temperature, the system is oftentimes referred to as a “dense fluid” or “super critical fluid” to distinguish it from normal vapor and liquid (see Figure 1 for carbon dioxide in December 2009 TOTM [1]).

Calculation Procedure:

The following step-by-step calculation procedure may be used to determine the pressure and temperature profiles in a pipeline considering the Joule-Thompson expansion effect and heat transfer between the pipeline and surroundings.

1. Divide the pipeline into n segments. The segments may be different lengths, but should be carefully chosen to provide the information sought through the calculations to be made. The more segments, the longer the calculation time. Time, however, is a relatively small investment compared to the importance of adequate representation of the line profile.
2. Assume an outlet pressure for each segment by use of a linear interpolation along the length of the line. Note that the outlet pressure of the first segment automatically becomes the inlet pressure to the second segment.
3. For the first iteration calculation, assume the flow in the segment is isothermal.
4. Calculate the average temperature, T_avg= (T_out + T_in)/2, and pressure, P_avg= (P_out + P_in)/2, for the first segment in the line. For the first iteration the inlet and outlet temperatures for the segment will be the same since isothermal flow is assumed.
5. Using the EOS, determine the state of the flow at T_avg and P_avg to establish whether or not the flow is in the dense phase.
6. Using the gas phase or liquid phase equations, calculate the segment pressure drop.
7. Compare the calculated pressure at the end of a segment with the pressure that was assumed in step 2. If the difference between these pressures is sufficiently small, proceed to step 8. If the difference between the assumed and calculated pressure at the end of segment is too large (1 psi or 6.9 kPa), replace the assumed outlet pressure with the calculated value of the outlet pressure and repeat steps 4 through 7 as many times as necessary to calculate s suitable segment outlet pressure.
8. Calculate the enthalpy at the end of the segment by writing an energy balance around the segment using the following procedure:
   H_out = H_in+ Q                        (1)
   Where:
   Q = UA (T_avg-T_s)                     (2)
   H_out= Enthalpy of the fluid at the outlet of the segment
   H_in= Enthalpy of the fluid at the inlet of the segmentQ = The overall heat transfer to or from the segment
   U = The overall heat transfer coefficient between the external surface of the pipe and its surroundings
   A = The external surface area of the segment of pipe
   T_avg = The average temperature of the segment
   T_s = The temperature of material surrounding the pipe
9. Using the EOS, determine the segment outlet temperature based on the calculated H_out and P_out.
10. If the temperature calculated in step 9 is the same as the assumed value in step 3, the calculations proceed to the next segment of the line. If the temperature is different from that assumed in step 3, calculations revert to step 4 using the newly calculated value for segment outlet temperature.

When conditions at the outlet end of the last segment of the line have been calculated to a satisfactory small difference (less than 1 psi or 6.9 kPa for pressure and less than 0.1 ˚F or 0.05 ˚C for temperature), calculations for flow conditions in the pipeline are complete.

In the following section we will illustrate the pressure drop calculations for transporting CO₂ in dense phase using the gas phase pressure drop equations. For details of pressure drop equations in the gas and liquid phases refer to the January 2012 TOTM [2].

Case Study:

For the purpose of illustration, we considered a case study [also described in reference 2] for transporting 160 MMSCFD (4.519×10⁶ Sm³/d) CO₂ using a 100 miles (160.9 km) long pipeline with an inside diameter of 15.551 in (395 mm). The corresponding mass flow rate is 214.7 lb_m/sec (97.39 kg/s). The inlet conditions were 2030 psia (14 MPa) and 104˚F (40˚C). The following assumptions were made:

1. Pure CO₂, ignored any impurities such as N₂.
2. Horizontal pipeline, no elevation change.
3. Five different inside surface relative roughness’s (roughness factor), ε/D, were studied (0.00004, 0.00013, 0.0002, 0.0004, and 0.001).
4. The ambient/surrounding temperature,Ts, is 55 ˚F and (12.8 ˚C)
5. Six different overall heat transfer coefficients ranging from 0 to 1 Btu/hr-ft²-˚F (0 to 5.678 W/m²-˚C) were studied.

Properties: The dense phase behavior and properties were calculated using the Span and Wagner CO₂  EOS [3] in ProMax [4] software. ProMax was also used to determine pressure and temperature profiles along the pipeline.

Results and Discussions:

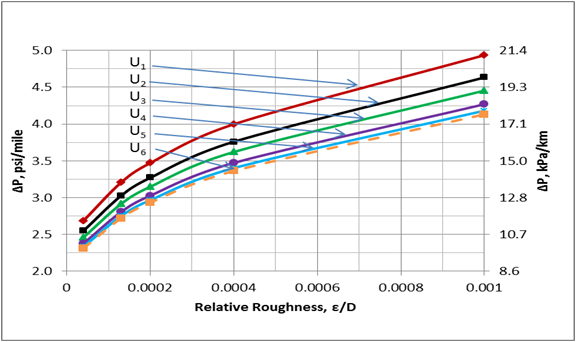
Figure 1 presents the pressure drop per unit length as a function of relative roughness (ε/D) and the overall heat transfer coefficient (U). In this figure, the values of U₁ through U₆ are 0, 0.125, 0.25, 0.5, 0.75, and 1.0 Btu/hr-˚F-ft² (0, 0.71, 1.42, 2.839, 4.259, and 5.678 W/m²-˚C), respectively.

Figure 1. Variation of pressure drop with the relative roughness and the overall heat transfer coefficient.

            Figure 1 indicates that as the overall heat transfer coefficient increases, pressure drop decreases. This is because the line temperature drops more quickly at higher overall heat transfer coefficients. Note that as the U approaches 1.0 Btu/hr-˚F-ft² (5.678 W/m²-˚C) its effect vanishes.

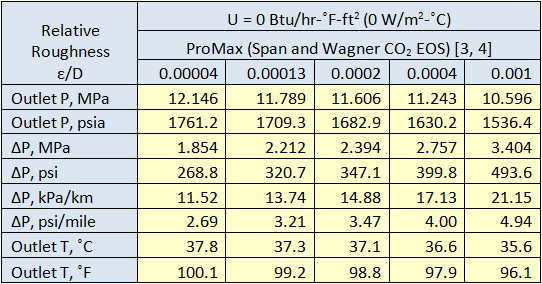
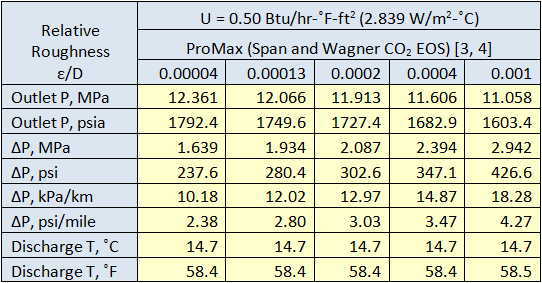
As an example, Tables 1 and 2 present the impact of relative roughness on the pressure drop for an overall heat transfer coefficient of 0 and 0.50 Btu/hr-˚F-ft² (0 and 2.839 W/m²-˚C), respectively. These tables also present the line outlet temperatures.

Table 1. Impact of relative roughness on pressure drop (Number of segments=10).

Table 2. Impact of relative roughness on pressure drop (Number of segments=10).

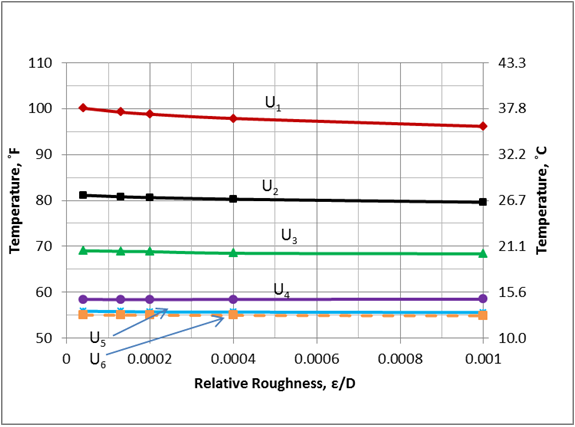
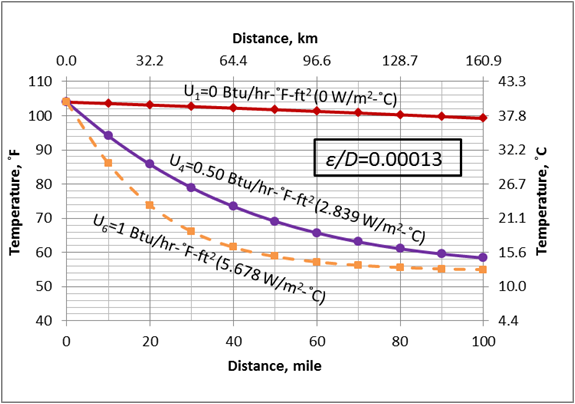
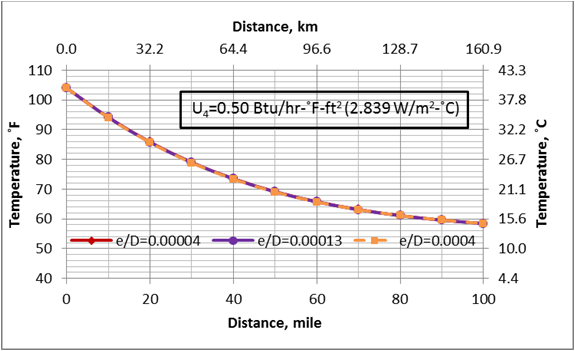
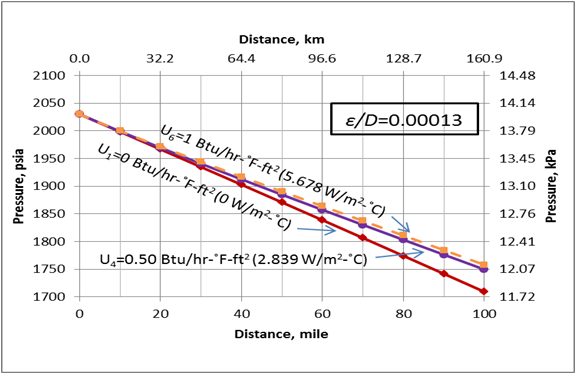
These two tables and Figure 2 indicate that while the relative roughness has great impact on the pressure drop, its effect on temperature is small. On the other hand, the effect of overall heat transfer coefficient on the outlet temperature is more significant. The impact of U on the line temperature profile is shown in Figure 3. This figure also indicates that U has great impact on the line temperature profile. Figure 4 also indicates that the effect of relative roughness on the line temperature is negligible. Figure 5 presents the effect of the overall heat transfer confident on the line pressure profile. As can be seen in this figure, the increase in the overall heat transfer coefficient results in lower pressure drop. This is because the line temperature drops more quickly at the higher values of overall heat transfer coefficients.

Figure 2. Variation of the outlet temperature with the relative roughness and the overall heat transfer coefficient.

Figure 3. Variation of temperature profile with the overall heat transfer coefficient

Figure 4. Variation of the temperature profile with the pipe relative roughness

Figure 5. Variation of the line pressure profile with the overall heat transfer coefficient

Conclusions:

Analyzing Tables 1 and 2 and Figures 1 through 5, the following conclusions can be made:

1. The effect of the overall heat transfer coefficient on the pipeline temperature is significant.
2. As the overall heat transfer coefficient increases, the outlet temperature decreases.
3. As the overall heat transfer coefficient increases, the outlet pressure increase (line pressure drop decreases).
4. As the value of the heat transfer coefficient approaches 1.0 Btu/hr-˚F-ft² (5.678 W/m²-˚C) its effect on the pipeline pressure drop vanishes.
5. While pipeline roughness factor has great impact on the pressure drop, it has little effect on the pipeline temperature profile.

To learn more about similar cases and how to minimize operational problems, we suggest attending our G40 (Process/Facility Fundamentals), G4 (Gas Conditioning and Processing), P81 (CO₂ Surface Facilities), and PF4 (Oil Production and Processing Facilities) courses.

John M. Campbell Consulting (JMCC) offers consulting expertise on this subject and many others. For more information about the services JMCC provides, visit our website at www.jmcampbellconsulting.com, or email your consulting needs to consulting@jmcampbell.com.

By: Dr. Mahmood Moshfeghian

Reference:

1. Bothamley, M.E. and Moshfeghian, M., “Variation of properties in the dese phase region; Part 1 – Pure compounds,” http://www.jmcampbell.com/tip-of-the-month/2009/12/variation-of-properties-in-the-dense-phase-region-part-1-pure-compounds/, December 2009.
2. Moshfeghian, M., ”Transportation of CO₂ in the Dense Phase,” http://www.jmcampbell.com/tip-of-the-month/
3. Span, R.; Wagner, W. – Equations of State for Technical Applications. I. Simultaneously Optimized Functional Forms for Nonpolar and Polar Fluids. Int. J. Thermophys. 2003,24(1), 1-39
4. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2011.