Existen varias herramientas en base de computadora desebadas específicamente para el modelaje y análisis de sistemas multifásicos complejos tales como el PipePhase, PipeSim, Olga, etc. (1). El modelaje y simulación de sistemas multifásicos, aun cuando en condición de flujo continuo, es complejo. En el previo del mes (PDM) de Junio, ilustramos como los programas de simulación de procesos pueden ser aplicados para simular una línea de transmisión de gas. Estos programas se basan en modelos mecanísticos, correlaciones desarrolladas en el laboratorio, y se confían en algorítmos iterativos complejos para proceder con los cómputos tediosos.
Sin embargo, para los cálculos efectuados a mano, la Correlación Flanigan (la cual se basa en líneas de transmisión dominadas por gas) ha sido desarrollada, y se puede aplicar usando cómputos manuales relativamente directos. Esta correlación se ha mostrado muy útil a pesar de su sencillez. La relación entre el gasto de gas, diámetro, y caída de presión se representa mediante la aplicación de la ecuación Panhandle A, la cual es aplicable para el flujo de gas. La ecuación básica se deriva de principios básicos, mientras que la Panhandle A, y la ecuación Flanigan se ajustan a un amplio rango de datos provenientes del campo. Dos correcciones se asimilan en la Ecuación Flanigan para en flujo bi – fásico:
- El valor de la presión de descarga es ajustada para las pérdidas provenientes del flujo cuesta arriba, y cuesta abajo de las dos fases, lo cual incluye el efecto de la retención del líquido.
- El término de eficiencia se correlaciona para reflejar el rendimiento medido del sistema basado en la velocidad del gas, y la relación liquido-gas.
Para el detalle de la ecuación Panhandle A, y la correlación Flanigan consulten al Capítulo del Vol. I de texto “Gas Conditioning and Processing” (2). Los algorítmos para la simulación por computación se discuten en el Volumen 3 , del “Gas Conditioning and Processing” , (3).
En éste PDM ( el cual es una continuación del de Junio) , demostraremos la certeza, y aplicación de la correlación Flanigan.
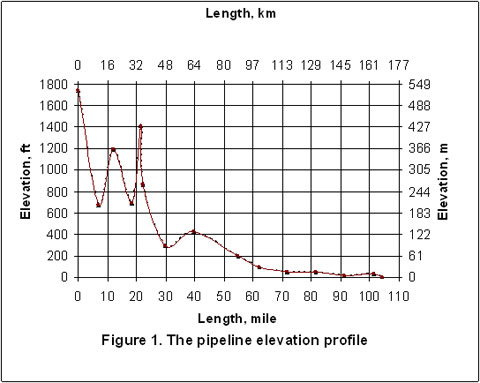
Consideremos el mismo caso que fuera analizado en PDM de Junio. La composición y condiciones del gas natural se muestran en la Tabla 1. El gas se admite a un gasoducto de 20 pul. con diametro interno de 18.81 pul. ( 47.8 cm) a un caudal de 180 MMPCSD, equivalentes a 19800 lbmol/hr ( 8989 kgmol/h). La longitud de la tubería, y su perfil de elevación se muestran en la Figura 1. La temperatura ambiental fue asumida en 60 ºF ( 15.6 ºC). El gas se admite a la línea a 1165 lpca ( 8032 kPa), y 95 ºF ( 35ºC). El caño se encuentra enterrado bajo tierra con un coeficiente total de intercambio de calor de 1 BTU/hr-pie2-ºF (5.68 W/m2-°C). Debido al alto contenido de H2S y CO2 (25.6 y 9.9 mole %, respectivamente), y para prevenir la corrosión mas la formación de hidratos, el gas ha sido deshidratado antes de ser admitido al caño.
Tres métodos aplicados en este análisis incluyen la ecuación básica de flujo (2), la correlación Flanigan, y otros modelos de computación aplicando la correlación Beggs-Brill con la relación original de la retención del líquido. La ecuación de estado (EOS) SRK fue aplicada para realizar los cómputos de equilibrio de fases basados en los análisis de computación.
La tubería fue dividida en 14 segmentos para coincidir con los números de ascensos de colinas, y sectores de descenso de las mismas. Adicionalmente, cada segmento fue dividido en 10 incrementos iguales, para lograr mayor certeza en la computación. Esta división no se requiere para la correlación Flanigan, y solo se efectúa para cumplir con la comparación de los demás modelos.
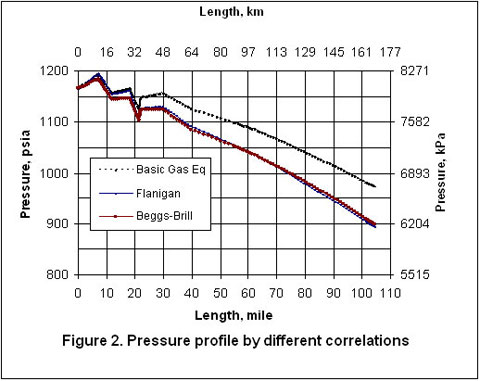
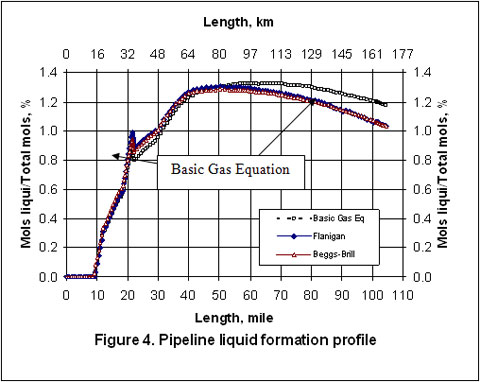
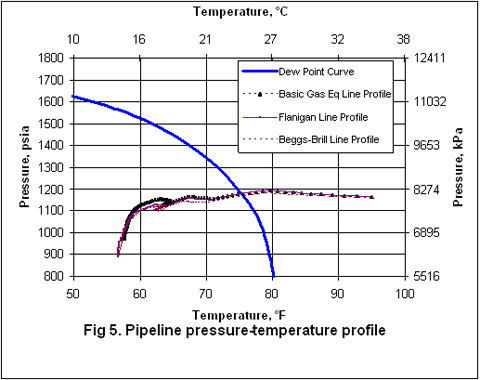
Las Figuras 2 al 5 presentan la presión, temperatura , y perfil de formación de líquidos a través del caño. La Figura 2 indica que los perfiles de presión arrojadas por Flanigan coinciden de manera cercana con los resultados obtenidos por análisis computacional de mayor rigor aplicando el método Beggs – Brill. Sin embargo, como es de esperar, debido a la presencia de la formación de líquidos en la línea, la ecuación básica de gas desvía algo de las correlaciones para las dos fases.
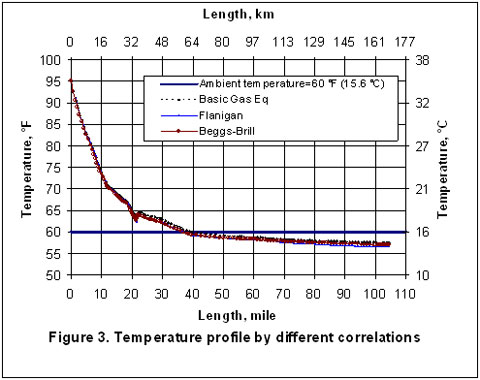
La Figura 3 indica que los perfiles de temperatura calculada por las tres correlaciones coinciden una con otra. La pequeña cantidad de condensación de líquido en la línea muestra un impacto menor en el perfil de temperatura que en el de presión. Los perfiles de formación de líquidos establecidos por las tres correlaciones se resumen en la Figura 4. Como mostrado por ésta, las cantidades estimadas por las correlaciones Flanigan y Beggs-Brill coinciden muy bien, pero la predicción para la formación de líquido presentada por la ecuación básica son distintas a aquellas presentadas por los otros dos modelos.
En este estudio, los mismos puntos de ebullición, densidad relativa, y peso molecular del C6+, como mostrados en la Tabla 1, fueron aplicados para las tres correlaciones. De esta manera, las misma propiedades críticas, y factor acéntrico fueron aplicados. Estas propiedades y los parámetros binarios interactivos son requeridos para lograr los cómputos de equilibrio de fases por una EDE (EOS) tal como la SRK. En adición, los mismos parámetros binarios interactivos entre los distintos componentes y el C6+ fueron aplicados.
El trabajo aca reportado indica claramente el valor de la correlación Flanigan, y como ésta puede ser utilizada para modelar y analizar el comportamiento de un gasoducto. Sin embargo, se debe tomar precauciones en utilizar esta correlación apropiadamente. Aun cuando la correlación Flanigan es sencilla, coincide con la mas rigorosa de Beggs – Brill. Esperamos, sin embargo, que estas similaridades entre las dos, se deterioren, mientras que el volumen de líquido formado en la línea aumente. Como esperado, la ecuación básica de gas predijo menores caídas de presión, debido a que ésta ignora la formación de líquidos. Aun cuando la ecuación Flanigan no es sensitiva a las correcciones de elevación, es importante incluir estos factores con un estimado razonable de la suma de las pendientes cuesta arriba, así como las cuesta abajo. Los resultados también son relativamente insensitivos al factor de eficiencia, de manera que valores ponderados para las relaciones líquido a gas pueden ser aplicadas para cada segmento.
Casos similares de flujo se discuten en nuestros cursos : Fundamentals of Onshore and Offshore Pipeline Systems – PL-4; Onshore Pipeline Facilities – Design, Construction and Operations – PL-42; Flow Assurance for Pipeline Systems – PL-61.
By: Dr. Mahmood Moshfeghian
Translated by Dr. Frank Ashford
References:
- Ellul, I. R., Saether, G. and Shippen, M. E., “The Modeling of Multiphase Systems under Steady-State and Transient Conditions – A Tutorial,” The Proceeding of Pipeline Simulation Interest Group, Paper PSIG 0403, Palm Spring, California, 2004.
- Campbell, J. M., and Hubbard, R. A., Gas Conditioning and Processing, Vol. 1 (8th Edition, 2nd Printing), Campbell Petroleum Series, Norman, Oklahoma, 2001.
- Maddox, R. N. and L. L. Lilly, Gas Conditioning and Processing, Vol. 3 (2nd Edition), Campbell Petroleum Series, Norman, Oklahoma, 1990.

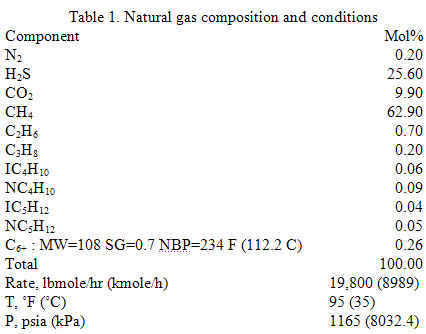
No comments
Trackbacks
By submitting a comment you grant Campbell Tip of the Month – Spanish a perpetual license to reproduce your words and name/web site in attribution. Inappropriate and irrelevant comments will be removed at an admin’s discretion. Your email is used for verification purposes only, it will never be shared.