En el Previo del Mes (TOTM) de Febrero 2007, Joe Honeywell [1] presento un procedimiento dirigido a calcular la caída de presión del fluido para el caso de un liquido en un sistema de cañerías debido a la fricción. Continuando con el PDM de Honeywell podemos bosquejar los procedimientos para calcular las caídas de presión en tuberías de petróleo y gas. Desde el punto de vista del Ingeniero, la pregunta pudiese surgir: “cuan sensible es la caída de presión causada por la fricción, al factor de rugosidad de la pared?” Es obvio que la respuesta es “depende”. Para explicar la respuesta en forma cuantitativa, y cualitativa, estudiaremos el efecto del factor de rugosidad de la pared del cano en dos [2] casos contenidos en este PDM. Para el primer caso en estudio, un oleoducto con gasto de 0.313 m3/s (170,000 bbl/dia), y el segundo , un gasoducto con caudal de 22.913 Sm3/s (70 MMPCSD) se estudiarán, y los resultados computacionales se presentarán en formato de grafico, asi como en tablas.
Factor de Fricción
El Diagrama Moody de la Figura 1 es una representación clásica del comportamiento de un fluido Newtoniano, y es aplicado a través de la Industria para pronosticar las perdidas en el transporte de los fluidos. Gráficamente representa los distintos factores usados para determinar el factor de fricción. Por ejemplo, los fluidos con numero Reynolds de 2000 o menor, el comportamiento del flujo se considera ser laminar estable, y el factor solo depende el numero Reynolds [2]. El factor de fricción, f, para el régimen Laminar es representado por:
Donde Re es el número Reynolds y se expresa como la relación a las fuerzas inerciales a las viscosas y es expresado matemáticamente como:
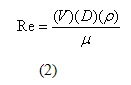
Fluidos con numero Reynolds entre 2000 y 4000 se consideran inestables, y pueden exhibir tanto el régimen laminar como el turbulento. Esta región usualmente se identifica como la zona critica, y el factor de fricción puede presentar dificultades en su predicción. Se debe aplicar juicio si se requieren predicciones acertadas en este régimen. Las dos ecuaciones 1, o 3 se usan comúnmente en la región crítica. Si el numero Reynolds es mayor que 4000, el fluido se considera parcialmente turbulento, o de turbulencia completa, y el factor de fricción depende en el numero Reynolds y la rugosidad relativa. Esto se observa para números Reynolds mayores a los 4000, donde el Diagrama Moody identifica dos regiones: la de transición, y la de turbulencia completa. El factor de fricción representativo en estas regiones se logra mediante la formula Colebrook, la cual es aplicada en toda las Industria, y representa acertadamente las regiones de transición y turbulencia del Diagrama Moody.
La fromula Colebrook para el número Reynolds mayor a 4000 se presenta en la ecuación 3 :

La ecuación Colebrook lleva dos términos. El primero, , (![]() )/3.7, es dominante par el transporte de gas donde el Re es alto. El segundo
)/3.7, es dominante par el transporte de gas donde el Re es alto. El segundo ![]() , es dominante para el transporte de fluido donde las líneas de rugosidad relativa convergen (caño liso). En la región de “Turbulencia Completa” las líneas son “planas”, indicando que son independientes del numero Reynolds. En la “zona de transición”, las líneas son función de Re y
, es dominante para el transporte de fluido donde las líneas de rugosidad relativa convergen (caño liso). En la región de “Turbulencia Completa” las líneas son “planas”, indicando que son independientes del numero Reynolds. En la “zona de transición”, las líneas son función de Re y ![]() . Cuando las líneas convergen en la “zona lisa”, el fluido es independiente de la rugosidad relativa.
. Cuando las líneas convergen en la “zona lisa”, el fluido es independiente de la rugosidad relativa.
Flujo liquido (Incompresible)
Para el caso de transporte de líquidos la ecuación 4, se ha aplicado por Ingenieros durante más de 100 años para calcular las caídas de presión en un cano debido a la fricción. Esta ecuacion relaciona varios parametros que contribuyen a la caída de presión. Esta es la forma modificada de la fórmula Darcy-Weisbach que fue derivada del análisis dimensional.

Flujo (Compresible) de Gas
Para el transporte del gas , la densidad es función primaria de la presión y temperatura, y esta pude variar considerablemente en el caño. Debido a las variaciones en la densidad , la ecuacion 5 debe ser aplicada para calcular la caída de presión en base a la fricción.
Una vez mas, el factor de fricción en esta ecuación se calcula mediante la relación 5 para un número Reynolds, y rugosidad relativa determinada, aplicando un ensayo iterativo. El volumen actual es requerido para calcular la velocidad del gas en la línea, factor que determina el numero Reynolds. La ecuación 6 puede ser aplicada para convertir el gasto a condiciones estándar, a las condiciones actuales.
Estudio Caso 1: Oleoducto
Consideren una línea de exportación de 16 pul (diámetro interno de 395 mm) para el transporte de 170,000 Bbbl/d (0.313 m3/s) de un crudo de43 API (densidad relativa de 0.81) desde una plataforma costa fuera hacia un terminal en tierra. La longitud del oleoducto es de 55 km. La temperatura ambiental es 5 °C y la viscosidad del crudo a la temperatura promedio es de 0.001 cP. La presión de alimentación de la línea es 14.9 MPa (absoluto). Como el propósito de este estudio es analizar el impacto de la rugosidad en la caída de presión, se ignoran los cambios de altura.
Para estudiar el efecto del factor de rugosidad sobre la caída de presión, ![]() fue variado desde 1x10-6 a 1x10-3. Un factor de
fue variado desde 1x10-6 a 1x10-3. Un factor de ![]() = 1x10-6 representa una tubería muy lisa.
= 1x10-6 representa una tubería muy lisa.
Estudio Caso 2: Gasoducto
Consideremos un gasoducto de 8 pul (diámetro interno de 190 mm) para manejar 70 MMPCS/D (22.913 Sm3/s) de un gas natural de peso molecular de 19.3 (densidad relativa de 0.67) desde una plataforma costa fuera a tierra. La longitud de la línea es de 43 km. La temperatura ambiental es 5°C y la viscosidad del gas a la temperatura promedio de la línea es 1.1x10-6 cP. La temperatura de alimentación es 35°C y la presión es 13.0 MPa (absoluta). Como el propósito de este estudio es analizar el impacto de la rugosidad en la caída de presión, se ignoran una vez más los cambios de altura.
Similar al caso del oleoducto, el factor de rugosidad ![]() fue variado desde 1×10-6 a 0.006. Nótese que para un factor de rugosidad mayor que .0006, una mayor presión, un diámetro incrementado, o caudal menor fue requerido. La caída de presión calculada como función del factor de rugosidad se presenta en la Figura 2. Para cada valor del factor de rugosidad, el cambio porcentual en la caída de presión comparado con una tubería muy lisa (
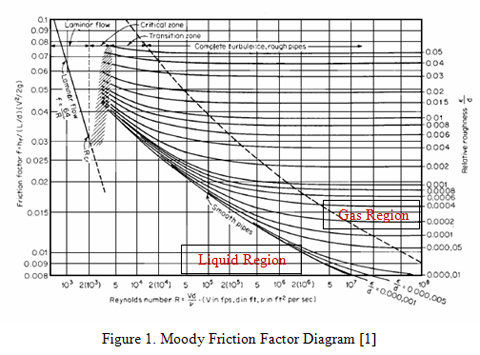
fue variado desde 1×10-6 a 0.006. Nótese que para un factor de rugosidad mayor que .0006, una mayor presión, un diámetro incrementado, o caudal menor fue requerido. La caída de presión calculada como función del factor de rugosidad se presenta en la Figura 2. Para cada valor del factor de rugosidad, el cambio porcentual en la caída de presión comparado con una tubería muy lisa (![]() = 1×10-6) fue calculada, con los resultados presentados en la Figura 3.
= 1×10-6) fue calculada, con los resultados presentados en la Figura 3.
Discusión y Conclusiones
El análisis de la Figura 2 indica que para un oleoducto, la caída de presión atribuida a la fricción es casi independiente del factor de rugosidad para el rango 1×10-6<![]() <1×10-4 , sin embargo , para un
<1×10-4 , sin embargo , para un ![]() >1×10-4, esta caída si se ve que aumenta con el
>1×10-4, esta caída si se ve que aumenta con el ![]() . Para este rango, las curvas del factor de fricción se aproximan unas a otras, de manera que el factor de fricción también se asemeja.
. Para este rango, las curvas del factor de fricción se aproximan unas a otras, de manera que el factor de fricción también se asemeja.
En contraste al oleoducto, la caída de presión en un gasoducto es una función importante del ![]() . Como se puede observar de la Figura 2, la caída de presión atribuida a la fricción aumenta precipitosamente con el factor de rugosidad. La Figura 3 indica la comparación del cambio porcentual entre la caída de presión por fricción del Oleoducto vs. Gasoducto como función del factor de rugosidad. Para las líneas de transporte de líquidos, la variación máxima es de 20% , pero para los gasoductos se observa la variación máxima en mas de 200% . Una vez mas, esto se aclara con referencia a la Figura 1. Para el Gasoducto. El numero Reynolds es mayor que le mismo para líneas de líquidos, siendo este rango normalmente 5×106<Re<1×108. Para este rango, las curvas del factor de fricción son disparejas, de manera que los factores de fricción divergen.
. Como se puede observar de la Figura 2, la caída de presión atribuida a la fricción aumenta precipitosamente con el factor de rugosidad. La Figura 3 indica la comparación del cambio porcentual entre la caída de presión por fricción del Oleoducto vs. Gasoducto como función del factor de rugosidad. Para las líneas de transporte de líquidos, la variación máxima es de 20% , pero para los gasoductos se observa la variación máxima en mas de 200% . Una vez mas, esto se aclara con referencia a la Figura 1. Para el Gasoducto. El numero Reynolds es mayor que le mismo para líneas de líquidos, siendo este rango normalmente 5×106<Re<1×108. Para este rango, las curvas del factor de fricción son disparejas, de manera que los factores de fricción divergen.
En resumen, los gasoductos se comportan en forma contraria a las tuberías de transporte de líquidos, y la aplicación de los conceptos del ducto liso puede incurrir en reducciones considerables de las perdidas de presión en ellas. Esto a su vez, reduce la inversión en las operaciones (OPEX). Por ende las corridas planificadas de marranos para lograr limpieza de las líneas, se implanta para axial reducir el factor de rugosidad. Las Empresas modernas de transmisión del gas agregan un revestimiento de Epoxy Fundido Fusionado Fusion Bounded Epoxy (FBE), por cuanto el gasoducto es sensible a la rugosidad. Esto reduce del OPEX a largo plazo, Debe notarse que mientras la tubería es mas lisa, mayor es la Inversión de Capital (CAPEX) , de manera que en análisis de costos debe efectuarse para las aplicaciones Ingenie riles.
Due to the sensitivity of gas pipelines to roughness factor and other operation parameters, there are numerous gas flow equations (e.g. Weymouth, Panhandle A and B, AGA) to best fit certain design conditions [1].
Debido a la sensibilidad de los gasoductos al factor de rugosidad, mas otros parámetros, existen numerosas ecuaciones de flujo (e.i. Weymouth, Panhandle A and B, AGA) para mejor lograr el ajuste a las condiciones de diseño [1].
Para informarse sobre casos similares , y como poder minimizar los problemas operacionales, le sugerimos asistir nuestros Eventos ME44 (Overview of Pumps and Compressors in Oil and Gas Facilities), ME46 (Compressor Systems – Mechanical Design and Specification), PL4 (Fundamental Pipeline Engineering), G40 (Process/Facility Fundamentals), G4 (Gas Conditioning and Processing), and PF4 (Oil Production and Processing Facilities).
By: Dr. Mahmood Moshfeghian
Senior Consultant , Instructor JMC
Traducción (Translation): Dr. Frank E. Ashford , Instructor
Consultor JMC
Reference:
- Honeywell, Joe, “Friction Pressure Drop Calculation,” Campbell Tip of the Month, Feb 2007
- Campbell, J. M., “Gas Conditioning and Processing, Vol. 1, the Basic Principals, 8th Ed., Campbell Petroleum Series, Norman, Oklahoma, 2001
- Menon, E.S, Piping Calculations Manual, McGraw-Hill, New York, 2005

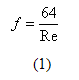


No comments
Trackbacks
By submitting a comment you grant Campbell Tip of the Month – Spanish a perpetual license to reproduce your words and name/web site in attribution. Inappropriate and irrelevant comments will be removed at an admin’s discretion. Your email is used for verification purposes only, it will never be shared.