Los programas de la simulación de Procesos son excelentes herramientas para el diseño, y evaluación de plantas de procesamiento, plantas químicas, refinerías de crudo, o líneas de transmisión de fluidos. En estos programas de simulación la mayoría de las propiedades termodinámicas se calculan mediante una ecuación de estado (EDE). Las ecuaciones de estado cúbicas se pueden considerar como lo principal de estos programas para la generación de las propiedades requeridas. Sin embargo, ninguna de estas son infalibles, y algún tipo de entonación debe efectuarse antes de iniciar su aplicación. Algo de esto se ha logrado por los investigadores, y ha sido configurado dentro de la base de datos de estos programas de simulación.
Tratando con sistemas fuera de lo estándar, y los complejos, el usuario debe revisar la validez y certeza del “paquete” termodinámico seleccionado (e.i. EDE), dentro de los programas de simulación antes de intentar efectuar dichas simulaciones. A menudo el usuario observa que se requiere la entonación. Esto se puede lograr efectuando una serie de cómputos de equilibrio de fases (EDF) tales como el punto de rocío, punto de burbuja, o equilibrio instantáneo, comparando estos con la información recogida del campo, o data experimental. Si la certeza no se ubica dentro de un rango aceptable, la EDE debe entonarse para actualizar esta. Esta entonación se puede lograr de varias maneras, pero la aplicada en forma mas común involucra el ajuste/regresión de los coeficientes binarios interactivos, entre pare binarios, y la mezcla que integra la data PVT, o EDE experimental.
En este Previo del Mes (PDM), demostraremos como los parámetros binarios interactivos se entonan en un programa de simulación para mejorar la certeza de una EDE seleccionada. Para este fin, demostraremos como la puntualidad para la predicción de un punto de burbuja para un sistema ternario de Dióxido de Carbono, Pentadecano, y Hexadecano pueden ser mejorados. Aplicaremos la ecuacion de estado Peng Robinson, PR, [1] incluida en el programa ProMax [2], y la data experimental EDE publicada en la literatura [3]. El mismo procedimiento puede ser aplicado con cualquier EDE dentro de otros programas de simulación.
La EDE PR
La EDE PR [2] expresada en términos de presión (P), volumen (v), y temperatura (T), se define como sigue:
Los valores de los parámetros a, y b deben ser estimados de manera especial para las mezclas. Cualquier ecuación, o serie de ecuaciones, empleadas para obtener parámetros de mezclas se denomina una regla de combinación, oregla de mezclas. Independientemente de la forma exacta de los cómputos, estos se basan en la premisa que las propiedades de la mezcla es alguna suma ponderada de las propiedades de la moléculas individuales que ntegran la mezcla.
Las reglas para las mezclas aplicadas en las ecuación de estado cúbicas ( e. i. Peng – Robinson, Soave – Redlich – Kwong, y Van der Waals) son
Donde:
a y b = la energía de interacción y parámetros de dimensión molecular para la Mezcla
ai, bi = parámetros a , b para el componente i de la mezcla
xi = composición (fracción molar) para el componente i de la mezcla
kij = parámetro de interacción binaria
n = numero de componentes en la mezcla
R = constante Universal del gas
Los ai y bi para cada componente en la mezcla son calculados en función de la temperatura critica (Tci), presión (Pci), y factor acéntrico, (?i) como presentado en las ecuaciones 4, y 5..
Una vez que a , y b han sido determinado, los cómputos de las ecuaciones de estado proceden como si a y b fuesen representativos de un componente puro. Con ecuación de estado cúbicas las reglas para las mezclas suman la propiedades basadas un parejas binarias.
El parámetro de interacción binaria kij no posee base teórica. Este es empírico y se aplica para vencer las deficiencias en el teorema de estados correspondientes o el modelo básico ( ecuación de estado). Los parámetros de interacción binaria son interpretados por regresión de la data experimental para un modelo especifico y deben ser aplicados solo para ese modelo. En adición, los kij pueden determinarse de un regresión de la información PVT, o ELV. Esto resultará en distintos kij para la misma mezcla binaria.
El efecto de kij en la predicción del Punto de Burbuja
Para estudiar el efecto del kij , la presión de punto de burbuja de una mezcla binaria de CO2 (1) , pentadecano (2) a 40 ° C para una serie de porcentajes molares ( mol. %) en la fase liquida fueron estimadas aplicando la EDE PR en ProMax. Primero se aplico el valor por defecto de la interacción binaria en la base de datos (BD) de ProMax, en el cual k12 fue usado. Los resultados pronosticados fueron comparados con data experimental y la desviación absoluta porcentual ponderada (DAPP) para ocho puntos de información de computo en un 41.06 %. Este DAPP se redujo a 1.64 % cuando el parámetro de interacción binaria k12 = 0.112 fue empleado. La Figura 1 presenta el efecto de k12 en el punto de burbuja predicho para la mezcla de CO2 y pentadecano. La Figura demuestra claramente el rol de kij en la mejora de la certeza para el cómputo del punto de burbuja. Esta mejora es sustancial, y la certeza ahora es tan buena como la data experimental.
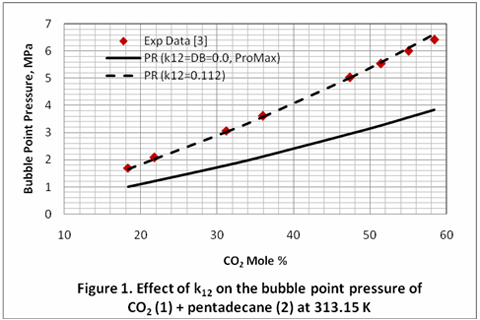
Mejoras similares fueron observadas cuando el parámetro de interacción k12 , fue cambiado de cero, y el valor de facto en la base de datos ( k12 = DB) de ProMax a 0.112 para la mezcla binaria de CO2 (1), y hexadecano (2) a 40 ° C. Para este caso los DAPP fueron 40.65 %, 3.64%, y 1.26% para k12 = 0.0 , k12 DB , k12 = 0.112 respectivamente.
Para estos dos sistemas la densidades del liquido igual fueron predecidas y comparadas con los valores experimentales. Para el sistema binario CO2 y pentadecano, el DAPP calculado para las densidades del liquido fueron 6.10 % , 6.36 % , para k12 = 0.0, y k12 = 0.112 respectivamente. Cambios del DAPP fueron observados para las mezclas binarias de CO2 y hexadecano .
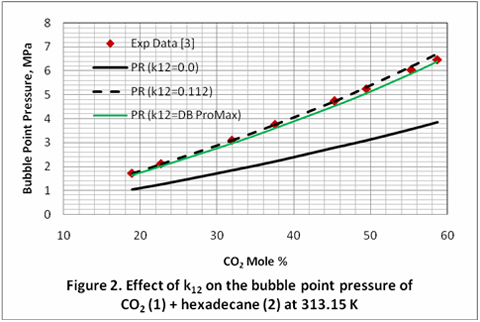
Normalmente, los parámetros de interacción binarios obtenidos de la regresión de mezclas binarias de infamación VLE arrojan buenos resultados en sistemas multicomponentes. Esto se demuestra usando los mismos kijs en una mezcla ternaria. Los parámetros de interacción binaria obtenidos de CO2 + pentadecano + hexadecano fueron aplicado sin cambios adicionales para predecir el punto de burbuja de las mezclas ternarias de CO2 + (1) pentadecano (2) , hexadecano (3). La Figura 3 indica que los parámetros binarios interactivos obtenidos de las mezclas binarias individuales mejoran considerablemente la certeza de las EDE . Similar al caso de las mezclas binarias, cuando los parámetros de interacción binarios k12, k13 fueron cambiados de cero, y el valor en defecto de la base de datos ProMax (kijs =DB) a 0.112 para la mezcla ternaria de CO2 + pentadecano + hexadecano a 40 °C, los DAPP fueron reducidos de 40.99%, y 25.16% a 1.75 % respectivamente.
Discusión y Conclusiones
Ha sido mostrado que los parámetros de interacción binarios de una EDE pueden ser ajustados/entonados/regresionados para mejorar considerablemente la certeza de los cómputos EDF . También ha sido demostrado que cuando los parámetros interactivos binarios fijados por regresión basados en data experimental EDF, y usados sin cambios adicionales en un sistema multicomponente, se logran mejoras considerables.
Es práctica saludable revisar la certeza de un conjunto de información termodinámica antes de ensayar cualquier simulación. Sin embargo, información experimental o de campo se requieren para cumplir con esta tarea.
Para instruirse adicionalmente sobre casos similares , y como ejecutar las simulaciones de procesos , sugerimos su asistencia a nuestro Eventos: G40(Process/Facility Fundamentals), G4 (Gas Conditioning and Processing) and G5 (Gas Conditioning and Processing – Special).
By: Dr. Mahmood Moshfeghian
Traducción al Español Por: Dr. Frank E. Ashford
References:
- Peng, D.Y. and Robinson, D.B., “A New Two-Constant Equation of State,” Ind. Eng. Chem., Fundam., Vol. 15, No. 1, P. 59, 1976.
- ProMax, V. 3.0, Bryan, Tex.: Bryan Research & Engineering Inc, 2009.
- Tanaka, H., Yamaki, Y. and Kato, M., “Solubility of Carbon Dioxide in Pentadecane, Hexadecane, and Pentadecane + Hexadecane,” J. Chem. Eng. Data,38, 386-388,1993.

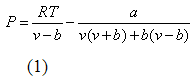
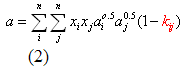
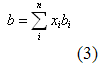
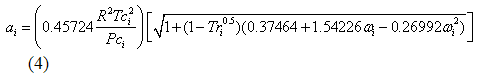
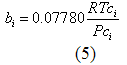
No comments
Trackbacks
By submitting a comment you grant Campbell Tip of the Month – Spanish a perpetual license to reproduce your words and name/web site in attribution. Inappropriate and irrelevant comments will be removed at an admin’s discretion. Your email is used for verification purposes only, it will never be shared.